[Algorithm] – “이진 탐색 트리(Binary Search Tree)”
[Algorithm] – “이진 탐색 트리(Binary Search Tree)”
이진 탐색 트리(Binary Search Tree) 의 개념
우리는 앞서 이진 탐색에 대해서 알아봤습니다. 위에서 소개한 알고리즘은 입력 리스트가 배열에 저장된 경우로 가정하고 있고, 이진 탐색은 배열이 정렬된 상태여야 적용이 가능하기 때문에 데이터의 삽입이나 삭제를 하기 위해서는 정렬된 상태를 유지하기 위한 데이터 이동 시간(O(n)) 이 필요했습니다.
우리의 똑똑한 선배님들께서는, 입력 리스트를 트리 형태로 유지함으로서 삽입과 삭제, 탐색이 용이한 자료구조를 생각해 내셨는데 그것을 이진 탐색 트리라고 합니다.
이진 탐색 트리는 아래의 성질을 만족합니다.
- 한 노드의 왼쪽 서브트리에 있는 모든 키값은 그 노드의 키값보다 작다.
- 한 노드의 오른쪽 서브트리에 있는 모든 키값은 그 노드의 키값보다 크다.
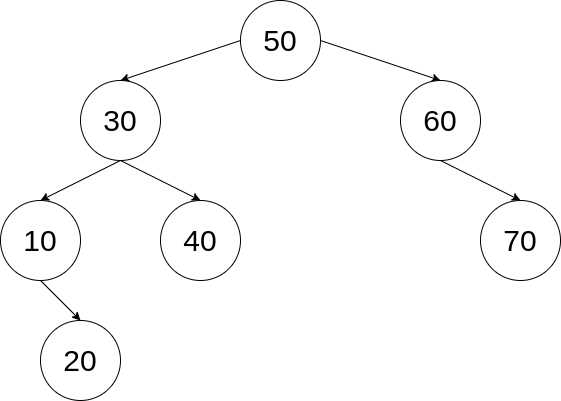
예컨대 위는 이진 탐색 트리입니다. 루트 노드부터 모든 노드를 살펴보면 각 노드의 왼쪽 서브트리에 있는 모든 키값은 그 노드의 키값보다 작고, 오른쪽 서브트리의 경우는 반대를 만족합니다.
이진 탐색 트리의 탐색 연산
이진 탐색 트리의 탐색 연산은 루트 노드에서부터 원하는 키값을 가지는 원소를 찾아나가는 방식입니다. 찾고자 하는 키 값과 루트 노드의 값에 따라서 왼쪽, 오른쪽으로 탐색해 나가면 되죠. 이전에 살펴본 이진 탐색 방식과 굉장히 유사한 방식입니다.
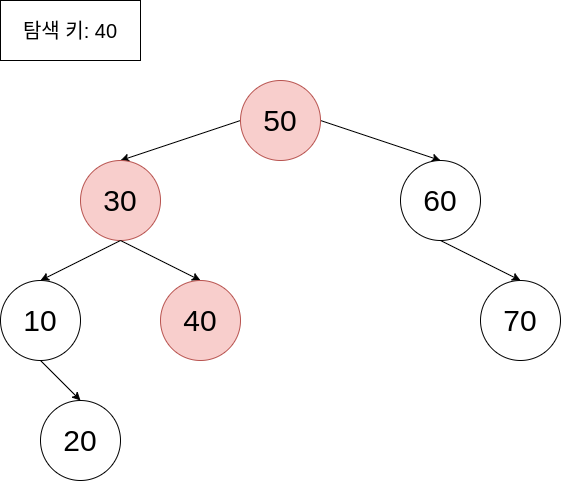
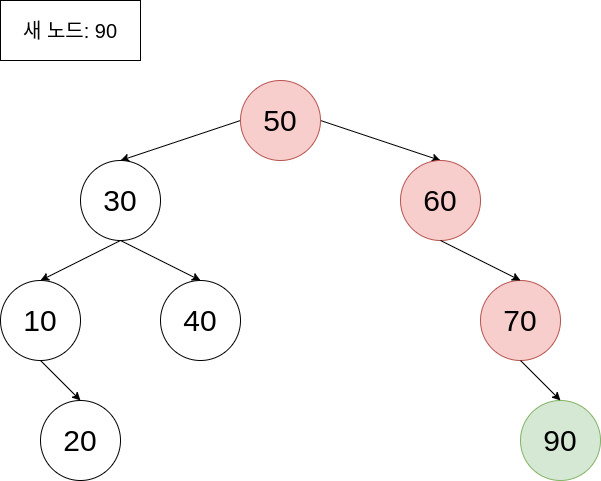
이진 탐색 트리의 삽입 연산
이진 탐색 트리에서 삽입은 아래의 순서로 이루어집니다.
- 이진 탐색 트리에서 삽입하고자 하는 값이 이미 존재하는지 확인합니다.
- 탐색이 실패하면, 해당 위치에 새로운 노드를 자식 노드로 추가합니다.
이진 탐색의 삽입 연산과는 달리, 다른 노드를 움직일 필요가 없습니다.
이진 탐색 트리의 삭제 연산
이진 탐색 트리의 삭제는 아래의 순서로 이루어집니다. 핵심 개념은, 삭제할 원소를 탐색한 후 찾은 노드를 루트로 갖는 서브트리에 대해 루트 노드를 삭제하고 남은 노드들의 위치를 조정해 이진 탐색 트리가 되도록 하는 것입니다.
- 삭제할 원소를 탐색합니다.
- 찾은 노드를 삭제하고, 남은 노드들의 위치를 조절해 이진 탐색 트리가 되도록 만듭니다.
- 자식 노드가 없는 경우, 남은 노드의 위치 조절을 하지 않아도 됩니다.
- 자식 노드가 하나인 경우, 자식 노드를 삭제되는 노드의 위치로 올리며, 서브트리 전체도 따라 올립니다.
- 자식 노드가 두 개인 경우, 삭제되는 노드의 후속자 노드, 혹은 선행자 노드를 삭제되는 노드의 위치로 옮깁니다. 대신, 이제부터 후속자(선행자) 노드가 삭제되는 노드가 되어 후속자(선행자) 노드의 자식 노드의 개수에 따라 위의 1, 2번으로 처리합니다.
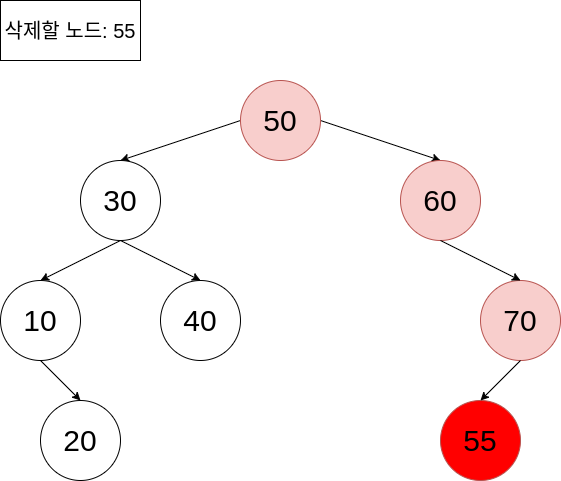
위처럼 자식 노드가 없는 노드를 삭제하는 경우에는, 남은 노드의 위치 조절을 하지 않아도 됩니다. 탐색 연산을 수행하여 삭제할 노드를 찾고, 삭제해 버리면 되죠.
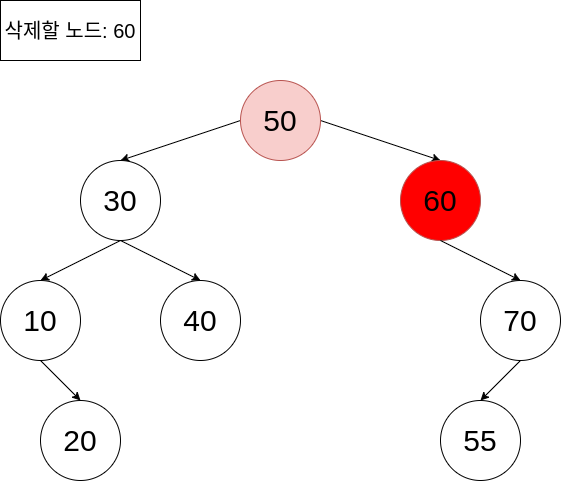
이 경우, 삭제되는 노드는 하나의 자식 노드를 가집니다. 자식 노드를 삭제되는 노드의 위치로 올리며, 서브트리 전체도 따라 올리면 됩니다.
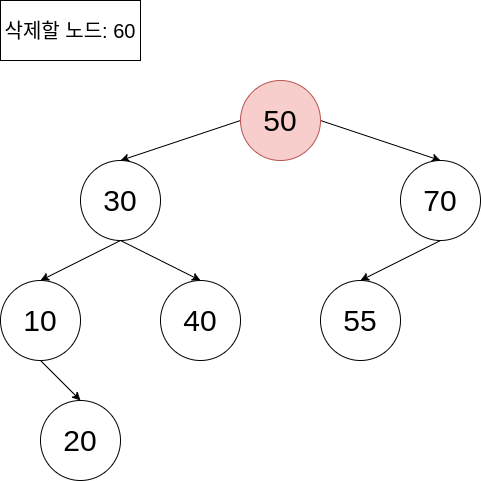
그러면 삭제할 노드의 자식 노드의 개수가 두 개인 경우에는 어떨까요?
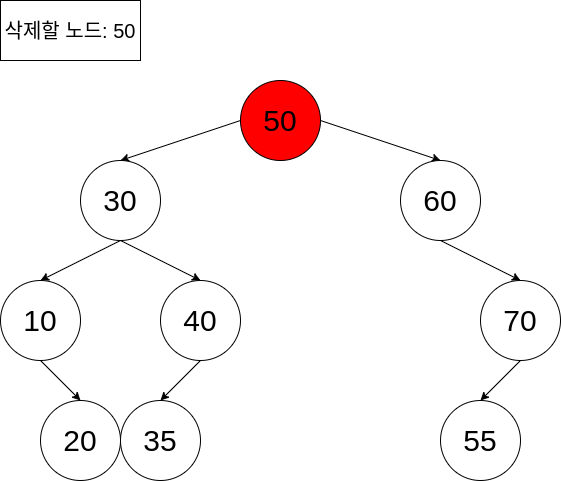
50이라는 키를 가지는 노드를 삭제해야 합니다. 이진 트리의 특성상, 아래에서 보시다싶이 삭제할 노드의 왼쪽 노드들의 값(노란색 부분)은 50보다 작고, 삭제할 노드의 오른쪽 부분(파란색 부분)의 모든 노드값들은 50보다 큽니다. 이는 50이 삭제된 이후, 이진 트리의 형태를 유지하기 위해 삭제된 자리에 30보다 크고 60보다 작은 값이 와야 한다는 것을 의미하기도 하죠.
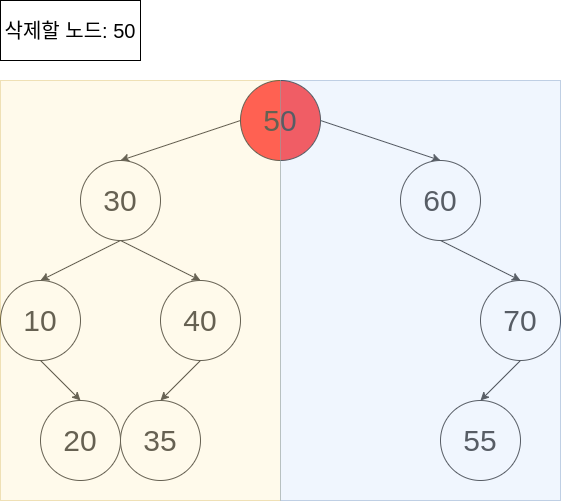
그러면 키값 50을 가지는 노드가 삭제되고, 저 자리에 위치할 수 있는 후보 노드들은 어떤 것들이 있을까요? 키값 35를 가지는 노드, 키값 40을 가지는 노드, 키값 55를 가지는 노드가 있겠네요. 이들은 모두 30보다 크고, 60보다 작은 값 을 가집니다.
삭제되는 노드의 왼쪽 서브트리에서 두 번째로 큰 값, 35라는 키값을 가지는 노드를 삭제 대상 노드의 위치로 올려 보겠습니다. 하지만 이렇게 하게 되면 아래의 트리는 더 이상 이진 탐색 트리가 아니게 됩니다. 이진 탐색 트리의 형태를 유지하고자 한다면, 추가적인 원소의 이동이 필요합니다.
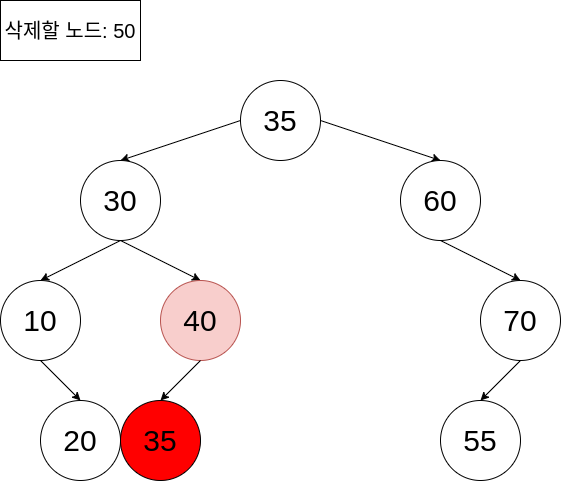
위의 형태가 이진 탐색 트리가 아닌 이유는 루트 노드 35를 기준으로 왼쪽의 모든 노드값이 35보다 작지 않기 때문입니다. 40은 35보다 크기 때문에, 이진 탐색 트리라고 할 수 없죠.
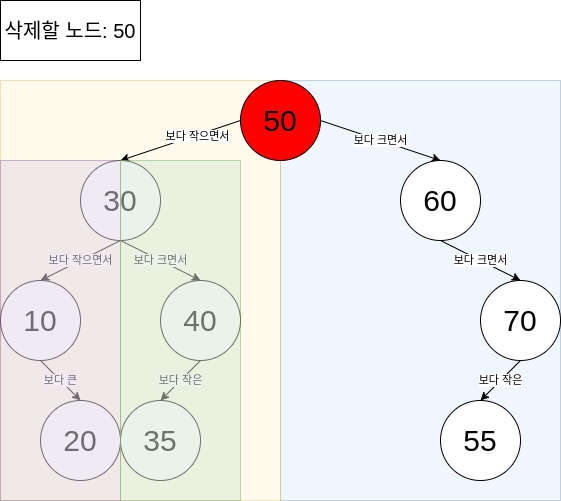
루트 노드부터 시작하여 내려가며 조건을 읽어 본다면 조금 더 쉽게 이해할 수 있습니다. 삭제되는 루트 노드에 왼쪽 서브트리에서 두 번째 로 가장 큰 값인 35가 위치한다면, 두 번째 라는 말 자체에서 이진 탐색 트리의 성질을 만족시키지 못한다고 할 수 있습니다. 왜냐하면, 이진 탐색 트리에서 왼쪽 서브트리에 있는 모든 노드값들은 해당 노드보다 작아야 하기 때문입니다. 결과적으로는 왼쪽 서브트리에서 가장 큰 노드값을 삭제하고자 하는 노드의 값으로 올려야 하는데, 그 노드를 선행자 노드라고 합니다.
오른쪽 서브트리의 경우에도 같습니다. 이진 탐색 트리에서 왼쪽 서브트리에 있는 모든 노드값들은 해당 노드보다 커야 하는데, 두 번째로 작은 노드를 삭제하고자 하는 노드값으로 올릴 경우 같은 이유로 이진 탐색 트리의 성질을 만족시키지 못하게 됩니다.
그러면, 결과적으로는..
- 왼쪽 서브트리에서 가장 큰 노드를 삭제하고자 하는 노드의 위치로 옮깁니다.
- 오른쪽 서브트리에서 가장 작은 노드를 삭제하고자 하는 노드의 위치로 옮깁니다.
가 되는 것입니다.
예제에서는 왼쪽 서브트리에서 가장 큰 노드를 삭제하고자 하는 노드의 위치로 옮기겠습니다.
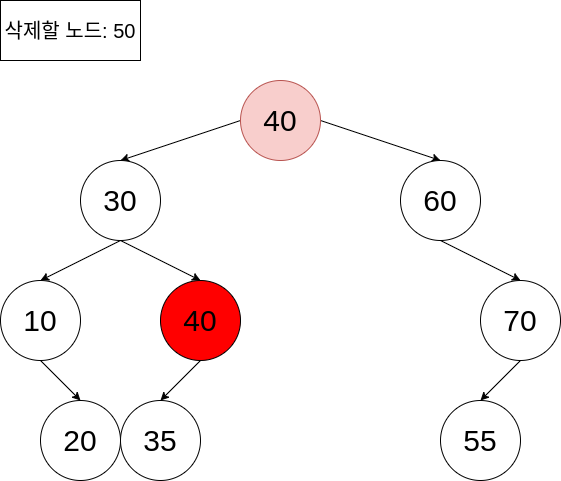
이 경우에서, 이제 삭제하고자 하는 노드는 아래쪽의 40 노드가 됩니다. 위에서 우리는 자식 노드가 하나만 있는 노드를 삭제하는 방법을 배웠습니다. 자식 노드를 삭제하고자 하는 노드의 위치로 옮겨 주고, 그 서브트리들도 모두 옮겨 주면 되었죠.
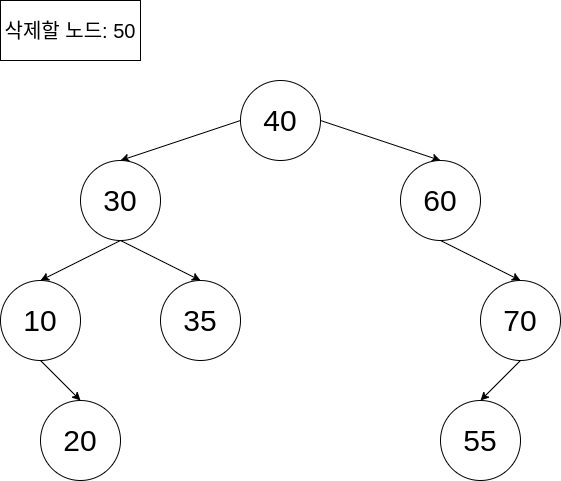
결과적으로, 아래와 같이 이진 탐색 트리에서 자식 노드가 2개인 노드의 삭제 연산을 수행할 수 있습니다.
이진 탐색 트리의 Python 구현
Python 으로 이진 탐색 트리를 아래와 같이 구현할 수 있습니다.
from typing import Optional
class Node:
def __init__(self, key: int):
self.left: Optional["Node"] = None
self.right: Optional["Node"] = None
self.key: int = key
def __str__(self) -> str:
return f"Node({self.key})"
class BinarySearchTree:
def __init__(self):
self.root: Optional[Node] = None
def find(self, key: int) -> Optional[Node]:
return self._find(self.root, key)
def insert(self, key: int) -> None:
if not self.root:
self.root = Node(key)
else:
self._insert(self.root, key)
def delete(self, key: int) -> None:
self.root = self._delete(self.root, key)
def _find(self, node: Optional[Node], key: int) -> Optional[Node]:
if node is None or node.key == key:
return node
if key < node.key:
return self._find(node.left, key)
return self._find(node.right, key)
def _insert(self, node: Node, key: int) -> None:
if key < node.key:
if not node.left:
node.left = Node(key)
else:
self._insert(node.left, key)
else:
if not node.right:
node.right = Node(key)
else:
self._insert(node.right, key)
def _delete(self, node: Optional[Node], key: int) -> Optional[Node]:
if node is None:
return node
if key < node.key:
node.left = self._delete(node.left, key)
elif key > node.key:
node.right = self._delete(node.right, key)
else:
if node.left is None:
return node.right
elif node.right is None:
return node.left
temp = self._min_value_node(node.right)
node.key = temp.key
node.right = self._delete(node.right, temp.key)
return node
def _min_value_node(self, node: Optional[Node]) -> Optional[Node]:
current = node
while current is not None and current.left is not None:
current = current.left
return current
def __str__(self) -> str:
return self._str_helper(self.root, "", True)
def _str_helper(self, node: Optional[Node], prefix: str, is_tail: bool) -> str:
if node is None:
return ""
result = f"{prefix}{'└── ' if is_tail else '├── '}{node.key}\n"
new_prefix = prefix + (" " if is_tail else "│ ")
if node.right:
result += self._str_helper(node.right, new_prefix, False)
if node.left:
result += self._str_helper(node.left, new_prefix, True)
return result
이진 탐색 트리의 탐색 연산 동작 과정
def find(self, key: int) -> Optional[Node]:
return self._find(self.root, key)
def _find(self, node: Optional[Node], key: int) -> Optional[Node]:
if node is None or node.key == key:
return node
if key < node.key:
return self._find(node.left, key)
return self._find(node.right, key)탐색 연산은 위의 논리 그대로, 루트 노드부터 시작해 키가 현재 노드의 키보다 작으면 왼쪽 하위 트리에서 찾고, 키가 현재 노드의 키보다 크면 오른쪽 하위 트리에서 찾습니다. 이 과정을 키를 찾거나, 더 이상 탐색할 하위 트리가 없을 때까지 반복합니다.
이진 탐색 트리의 삽입 연산 동작 과정
def insert(self, key: int) -> None:
if not self.root:
self.root = Node(key)
else:
self._insert(self.root, key)
def _insert(self, node: Node, key: int) -> None:
if key < node.key:
if not node.left:
node.left = Node(key)
else:
self._insert(node.left, key)
else:
if not node.right:
node.right = Node(key)
else:
self._insert(node.right, key)삽입 연산은 위와 같이 구현할 수 있는데, 루트 노드가 없는 경우 루트 노드를 초기화하고, 그렇지 않을 경우 아래의 논리에 따라 삽입을 수행합니다.
- 삽입할 키가 현재 노드의 키보다 작으면 왼쪽 하위 트리에 새 노드를 삽입합니다.
- 삽입할 키가 현재 노드의 키보다 크면, 오른쪽 하위 트리에 새 노드를 삽입합니다.
이진 탐색 트리의 삭제 연산 동작 과정
삭제 연산은 다음과 같이 구현될 수 있습니다.
def delete(self, key: int) -> None:
self.root = self._delete(self.root, key)
def _delete(self, node: Optional[Node], key: int) -> Optional[Node]:
if node is None:
return node
if key < node.key:
node.left = self._delete(node.left, key)
elif key > node.key:
node.right = self._delete(node.right, key)
else:
if node.left is None:
return node.right
elif node.right is None:
return node.left
temp = self._min_value_node(node.right)
node.key = temp.key
node.right = self._delete(node.right, temp.key)
return node- 삭제할 노드를 탐색해 찾습니다.
- 키가 현재 노드의 키와 일치하는 노드를 찾으면, 이 노드를 삭제합니다. 삭제할 노드의 자식 노드의 수에 따라 다음과 같이 처리합니다.
- 삭제할 노드가 자식 노드를 가지지 않는 경우: 그냥 노드를 삭제합니다.
- 삭제할 노드가 하나의 자식 노드만 가지는 경우: 삭제할 노드의 부모 노드가 삭제할 노드의 자식 노드를 가리키도록 합니다.
- 삭제할 노드가 두 개의 자식 노드를 가지는 경우: 삭제할 노드의 오른쪽 서브트리에서 가장 작은 노드(후계자 노드)를 찾아 삭제할 노드의 위치에 놓습니다. 그리고 이 후계자 노드를 오른쪽 서브트리에서 삭제합니다.
- 마지막으로, 삭제된 노드의 부모 노드를 반환합니다. 이는 삭제 연산 후에도 이진 탐색 트리의 속성을 유지하기 위함입니다.
이진 탐색 트리의 성능 분석과 특징
- 이진 탐색 트리의 높이가
h일 때, 탐색과 삽입/삭제의 시간 복잡도는O(h)입니다. - 이진 탐색 트리의 높이는 이진 탐색 트리의 형태에 따라
logn~n까지 가능합니다. 균형 이진 트리의 형태를 유지하는 경우O(logn)시감에 탐색과 삽입, 삭제가 가능하지만 모든 노드가 한 개씩의 자식 노드만을 가진 경사 트리의 경우라면O(n)시간이 필요합니다. - 이진 탐색 트리는 이진 탐색과는 다르게 삽입이나 삭제 연산 시 기존 노드의 이동이 거의 발생하지 않습니다.
- 이진 탐색 트리는 원소의 삽입과 삭제에 따라서 경사 트리 형태가 될 수 있습니다. 이 경우, 최악의 수행 시간을 가집니다.
