2-3-4 트리(2-3-4 Tree) 의 개념

[Algorithm] – “이진 탐색 트리(Binary Search Tree)”

우리는 지난 시간 이진 탐색 트리에 대해 알아봤습니다. 이진 탐색 트리는 균형 이진 트리 형태를 유지한다면 O(logn) 시에 탐색&삽입&삭제 연산을 수행할 수 있었지만, 아래와 같은 경사 트리의 형태라면 O(n) 시간이 필요했었습니다.

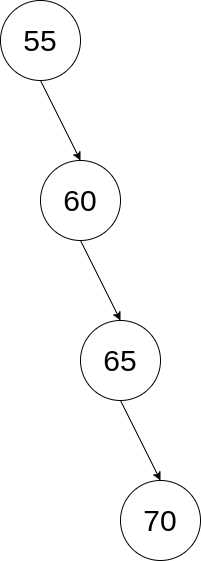
이진 탐색 트리는 맨 처음에 균형잡힌 형태를 보이고 있더라도, 삽입과 삭제를 거치며 얼마든지 위와 같은 경사 트리 형태가 될 수 있습니다. 입력 원소의 개수 n에 대해서 트리의 높이를 logn 으로 유지하지 못한다면, 최악의 수행 시간 O(n) 을 가지게 될 것이라는 의미이기도 합니다.

2-3-4 트리는 삽입, 삭제가 일어나더라도 경사 트리가 되지 않아 이진 탐색 트리의 장점을 유지할 수 있는 균형 탐색 트리입니다. 2-3-4 트리는 아래의 조건을 만족해야 합니다.

• 2-노드는 1개의 키, 2개의 자식을 갖는다.
• 3-노드는 2개의 키, 3개의 자식을 갖는다.
• 4-노드는 4개의 키, 4개의 자식을 갖는다.
• 각 노드의 한 키의 왼쪽 서브트리에 있는 모든 키값은 그 키값보다 작다.
• 각 노드의 한 키의 오른쪽 서브트리에 있는 모든 키값은 그 키값보다 크다.
• 모든 리프 노드의 레벨은 동일하다.

예를 들면, 아래의 트리는 2-3-4 트리입니다.

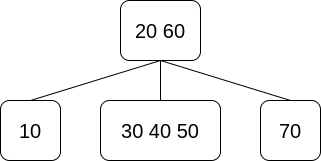
• 루트 노드는 2개의 키, 3개의 자식을 가집니다. (3-노드)
• 10, 70은 하나의 키로 구성된 2-노드입니다.
• 20의 왼쪽 서브트리의 모든 값 10은 20보다 작습니다.
• 60의 오른쪽 서브트리의 모든 값 70은 60보다 큽니다.
• 모든 리프 노드의 레벨은 1로 동일합니다.(루트 노드로부터의 거리)

이제 2-3-4 트리가 어떻게 각각 탐색&삽입&삭제를 수행하는지 알아보겠습니다.

2-3-4 트리의 탐색 연산

2-3-4 트리의 탐색 연산도 이진 탐색 트리의 탐색 연산과 비슷하게, 루트 노드부터 시작하여 탐색 키를 가진 원소를 찾아나가는 방식입니다.

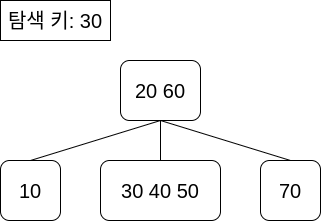
예를 들면, 위의 트리에서 탐색 키 30을 찾고자 한다면 아래의 과정을 거칩니다.

1. 루트 노드의 첫 번째 키값인 20과 탐색 키값인 30을 비교합니다. 30은 20보다 큽니다.
2. 루트 노드의 두 번째 키값인 60과 탐색 키값인 30을 비교합니다. 30은 60보다 작습니다.
3. 20 < 키값 < 60 이므로, 20과 60 사이에 있는 자식으로 내려갑니다. (30, 40, 50)
4. 해당 노드들의 키값 30과 비교하는데, 탐색 키와 일치하므로 탐색을 종료합니다.

2-3-4 트리의 삽입 연산

2-3-4 트리의 삽입 연산 또한 이진 탐색 트리의 삽입 연산과 비슷합니다. 삽입할 원소를 탐색 연산을 통해 탐색하고, 해당 원소가 없다면 현재 리프 노드에 키로 추가하는 방식이죠.

하지만, 탐색 중 4-노드를 만나면 항상 노드 분할이 먼저 발생한다는 것이 특징입니다. 분할은 4-노드 하나를 2-노드 세 개로 분할하는 것인데, 아래의 과정을 따릅니다.

• 가운데 키로 만든 2-노드를 부모 노드로 만듭니다.
• 나머지 2개의 2-노드가 자식 노드가 됩니다.
• 만약 분할되는 4-노드의 부모 노득 아씨다면, 가운데 키로 2-노드를 만드는 대신 그것을 부모 노드에 추가합니다.

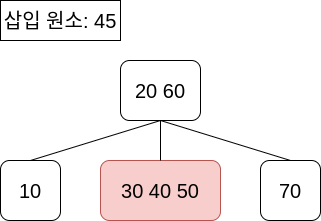
위의 예제를 살펴봅시다.

• 45를 삽입하기 위해 먼저 탐색 연산을 수행하는데, 그 과정에서 아래의 4-노드를 만나게 됩니다.
• 4-노드를 만났으므로 분할을 수행하게 됩니다.
  • 부모 노드가 존재하므로, 가운데 키 40을 부모 노드에 추가합니다.
  • 나머지 값(30, 50) 으로 2-노드를 만듭니다.

결과적으로, 아래처럼 45가 삽입됩니다.

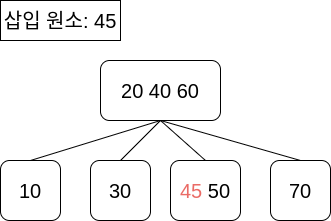
이제 이 트리에 30을 삽입해 봅시다. 루트 노드는 3-노드이므로 노드 분할을 수행합니다.

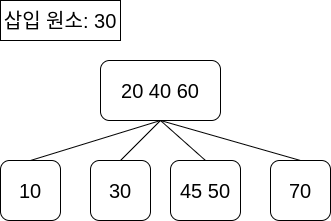
분할을 끝내면 아래와 같은데, 탐색 과정에서 같은 값 30을 찾았으므로 그대로 종료합니다.

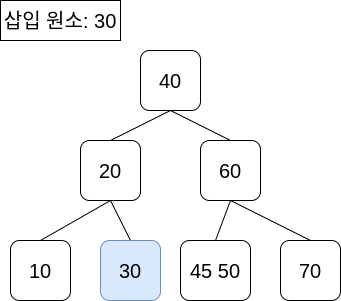
2-3-4 트리의 성능 분석과 특징

• 2-3-4 트리의 탐색, 삽입, 삭제 연산의 시간 복잡도는 O(logn) 입니다.
• 2-3-4 트리는 원소의 삽입과 삭제가 일어나도 경사 트리가 되지 않습니다.
  • 새로운 노드가 추가되는 경우는 노드 분할이 일어날 때, 부모 노드가 없는 경우일 뿐입니다. 루트 노드가 노드 분할이 되는 경우죠. 루트 노드가 1 늘어날 뿐이라, 모든 리프 노드는 동일하게 레벨이 1 증가하며 균형을 유지하게 됩니다.